Do you know how to use this graph?
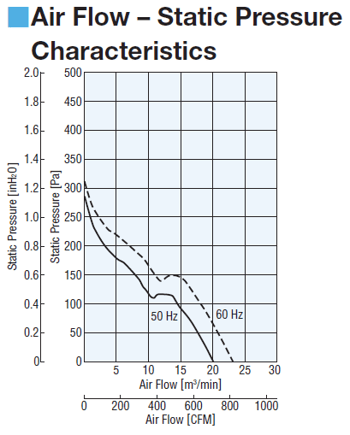
Similar to a motor's speed-torque curve, this graph is how manufacturers show the performance of their fans, and where the air flow and static pressure specifications come from.
For some customers, this may look completely foreign. Many customers I've dealt with in my past life as a technical support engineer selected fans based on dimensions and air flow. However, a deeper understanding is necessary to determine how the fan will actually perform in a real life scenario.
In this post, I will be discussing the definitions of air flow vs static pressure, the relationship between them, and the importance of impedance.
Airflow vs Static Pressure

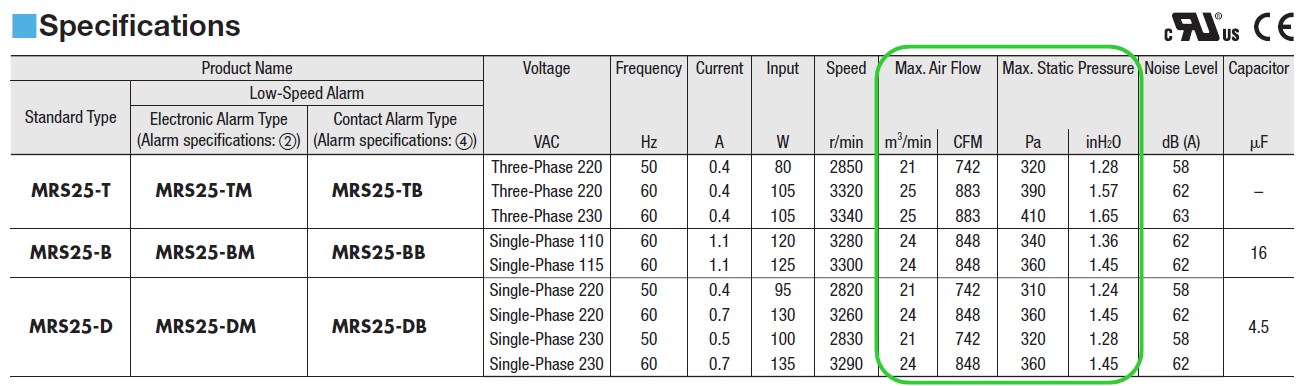
In the above fan specifications table, "Max. Air Flow" and "Max. Static Pressure" are listed as specifications.
Air flow is the volume of air that is produced by the fan measured by time. In this case, the air flow of a fan is measured in cubic meters per minute (m³/min) in metric units, or cubic feet per minute (CFM) in imperial units. In simplest terms, if you have a 5 ft x 5 ft x 5 ft enclosure, and a fan that produces 5 CFM, it will likely take 25 minutes for the fan to ventilate the hot air in the enclosure. (In actuality, it's not that easy.)
Static pressure is the amount of air pressure that can be produced by the fan in an enclosure. In this case, the static pressure is measured in Pascals (Pa), or inches of water (inH2O). The pascal (Pa) is the SI derived unit of pressure used to quantify internal pressure, stress...etc. The unit is named after Blaise Pascal and is defined as one newton per square meter. Inches of water (inH2O) is defined as the pressure exerted by a column of water of 1 inch in height at defined conditions. At a temperature of 4 °C (39.2 °F) pure water has its highest density (1000 kg/m³). At that temperature and the standard acceleration of gravity, 1 inH2O is approximately 249.082 pascals.
It's important to know that even though maximum values for air flow and static pressure are specified, the fan will not output both maximum values at the same time.
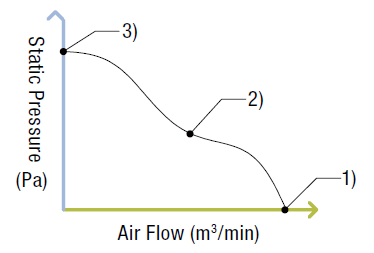
The relationship between air flow and static pressure of a fan is shown in the graph above. As you can see, air flow and static pressure have a negative correlation. When air flow increases, static pressure decreases; and when static pressure increases, air flow decreases. The 3 points depict possible scenarios where the fan will perform.
To visualize the 3 scenarios, you may have to imagine an electronics enclosure being ventilated by the fan. Refer to the graph above with the 3 designated points 1), 2), and 3).
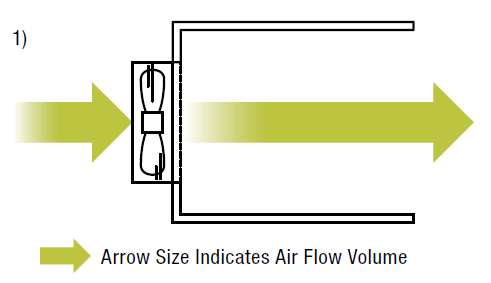
In example 1), we have an enclosure that is completely open on one end. There is nothing that obstructs the air flow from the fan, and all air flow is expelled out the other end. This example creates a scenario where maximum air flow would occur, and we have zero static pressure.
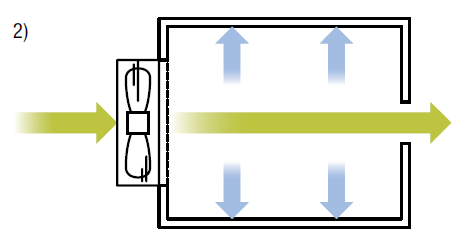
In example 2), we have an enclosure that is enclosed except with a small exhaust hole, or air outlet, on the other end. The size of the exhaust hole is smaller than the air intake hole, which hinders air flow. The constant build-up of air inside the enclosure not being able to escape increases the static pressure inside. This creates a scenario where air flow is limited by the increased static pressure. The air flow will be less than its maximum value.
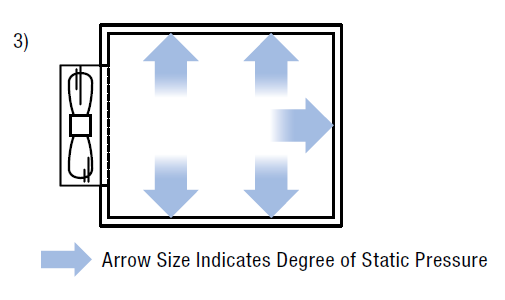
In example 3), the enclosure is completely closed. In this scenario, the airflow flowing into the enclosure causes the static pressure to rise since there's no place for the air to escape. Once the static pressure specification has been exceeded, even if the fan continues to operate, the high static pressure will not let any more air in. In other words, the maximum static pressure has been reached, and air flow volume drops to zero.
In real life, examples 1) and 3) are not realistic. In a practical example of ventilating an electronics enclosure, most fans would perform close to example 2). However, in order to produce the graph, a similar method is used (also known as the double chamber method).
Installation Density
OK now that we understand air flow and static pressure by using an electronics enclosure as an example, let's make it more realistic. An electronics enclosure houses critical electrical devices, such as PLCs, power supplies, and drivers for motion control within automated machines. Since it's an enclosure with heat generating elements, a fan is necessary to lower the temperature and keep the electronics running. The number of components inside an enclosure determines the "installation density".
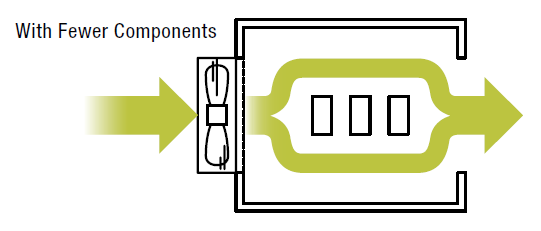
With fewer components (low installation density), there is more room for the air to pass through. This scenario would be somewhat close to example 1) above where the fan would produce high air flow.
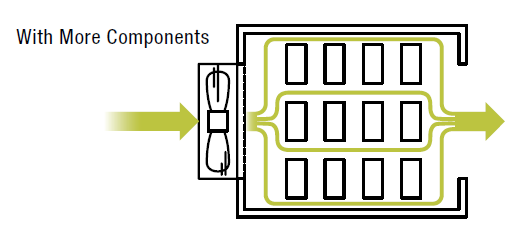
With more components (high installation density), there are more obstructions in the path of the air flow. This scenario would be similar to example 2) above, which is the most common. In this case, the high static pressure could decrease the air flow to below its maximum value.
The Importance of Impedance
How are the actual air flow and static pressure requirements determined? The answer is impedance. Impedance is defined as resistance to air flow, and it could be in the form of electronic components, walls, or anything that impedes the path of the air flow. The actual air flow and static pressure is determined by impedance.
Let's see how this is done. For most forced air cooling application, impedance is calculated by the "square law," which means that static pressure changes as a square function of changes in the CFM.
P = KrQn
where:
P = static pressure
K = load factor (here's some reference information)
r = Fluid Density
Q = Flow
n = constant; Let n=2; approximating a turbulent system.
In the graph below, we show 3 yellow lines to depict 3 different levels of impedance (A, B, and C).
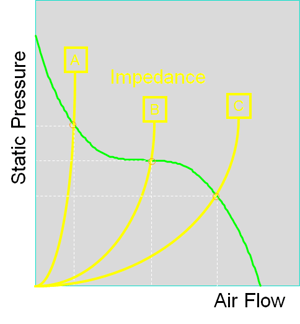
The green line depicts both air flow and static pressure. Point A depicts high impedance while point C depicts low impedance. The actual impeded air flow and static pressure are determined where the impedance curve (yellow) intersects the performance curve (green).
Sometimes, it can be difficult to determine system impedance. In this case, it can be safe to assume that the actual air flow will be about half of the fan's maximum air flow, so select a fan that can produce double the required air flow.
For a successful enclosure ventilation design, in addition to fan selection, other factors such as intake/exhaust hole size, location of holes, and placement of components, should be considered. In the following video, we use smoke to demonstrate how air flow can be affected by different enclosure designs, such as different intake hole diameters and the use of dividers.
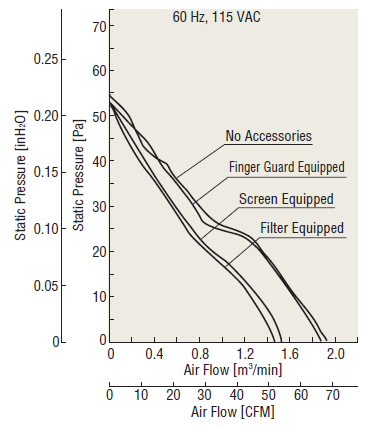
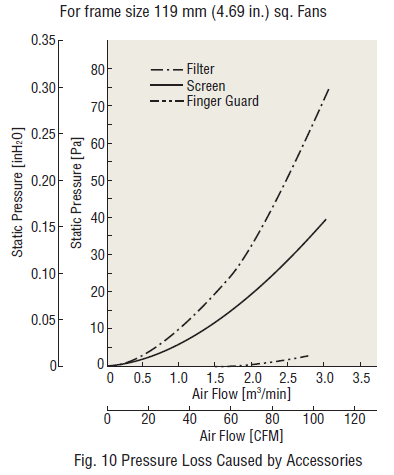
Using accessories such as filters, screens, or finger guards can increase the reliability and life of fans in dusty or wet environments, but they will also affect the air flow and static pressure characteristics.
 |
|
| The above graph shows data regarding pressure loss caused by fan accessories for a frame size 119 mm (4.69") fan. The filter causes the most significant pressure loss, while the finger guard causes little loss. | The above graph shows how characteristics may change with installation of accessories while using the MU1225S-21 fan as an example. Greater pressure loss causes greater reduction of air flow and static pressure characteristics. |
|
To learn more about fans, please refer to our Topics include: |