Besides load torque, acceleration torque, speed, and load inertia, overlooking certain sizing parameters during the motor sizing process can literally make or break your machine.
A motor's performance characteristics are described by its torque and speed specifications. A motor's structural strength is described by its radial load and axial load specifications. A motor's torque and speed specifications indicate if a motor can perform a task. A motor's radial load and axial load specifications indicates how long the motor can perform the task.
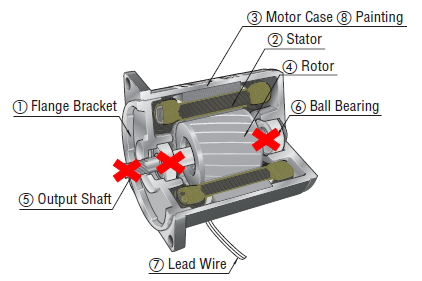
The structural strength of a motor comes from the combined mechanical rigidity of its case, flange brackets, and output shaft assembly. For a gear motor, it also includes the gears and additional bearings. However, the bearings located closest to the load "bear" most of this burden. Needless to say, the radial and axial load specifications of a motor or gearhead has a lot to do with its bearings.
We show the internal structure of an AC motor and its gearhead below. The same axial load and radial load concepts apply to all types of motors.
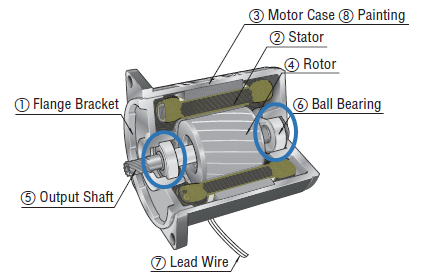 |
Let's start from inside out. A motor's only rotating element is the rotor (4) and shaft (5) assembly, which are supported by two ball bearings (6) on either end. Outside the rotor and separated by a very thin air gap is the stator (2). The flange bracket (1) and the motor case (3) complete the outer structure. The entire assembly supports all the static and dynamic forces within the motor at its rated load. |
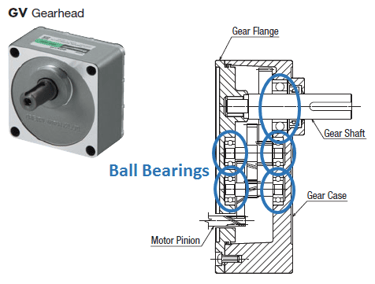 |
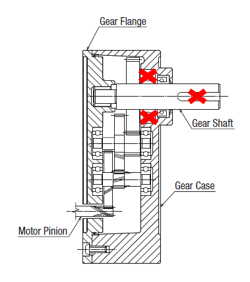
In a gearhead (or gearbox) that is fitted onto the motor's pinion shaft, each toothed gear and output shaft is supported by its own bearing, while the input shaft (motor pinion) is still supported by the motor bearing. Notice that the bearing supporting the gear shaft (and load) is the largest. The gear flange and gear case complete the outer structure. The entire assembly supports all the static and dynamic forces within the gearhead at its rated load. |
The output shaft bearing in the gearhead is typically bigger than the output shaft bearing in the motor because the load on the gearhead shaft would be much bigger than the load on the motor shaft.
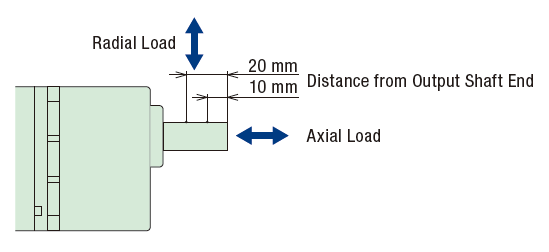
The images below shows an illustration of both radial load (overhung load) and axial load (thrust load) forces acting on a shaft of a motor and a gearhead.
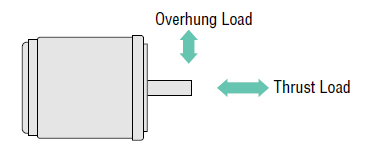
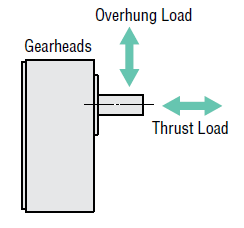
| Radial Load (also known as Overhung Load) |
Radial Load is defined as the maximum force that can be applied to the shaft in the radial direction (any direction perpendicular to the motor shaft axis). Radial load is also referred to as the "overhung load" because of how the load may "hang" off the shaft. Radial loads vary by the distance between the installation point of the overhung load to its support bearing.
| Axial Load (also known as Thrust Load) |
Axial Load is defined as the maximum force that can be applied to the shaft in the axial direction (in the same axis as or parallel to the motor shaft axis). Axial load is also referred to as the "thrust load" since thrust force and thrust load are forces acting upon the exact same axis. A typical axial load is about half the motor weight, although that has increased over the years.
These forces can act in any direction.
For example, if a motor has a 100 N axial load specification, it means that the motor can hang a 100 N load from its shaft (if the shaft is facing down), or support a load on its shaft (if the shaft is facing up). 100 N (Newtons) equates to about 10 kg.
| Why Are These Specifications Important? |
Both radial and axial load specifications are related to the strength, or mechanical rigidity, of the bearings, shaft, and case assembly. Exceeding these specifications may result damaging the ball bearings, such as flaking from the raceway and rolling elements, or breaking the output shaft.
 |
 |
For example, if the permissible radial load is exceeded, then the shaft may start bending and ultimately break. If the permissible axial load is exceeded, then the motor or gearhead bearing may deteriorate and ultimately fail. Either way, the motor would cease operation or suffer decreased life. The supporting element closest to the load is typically the first component to break.
|
TIP: Simple ball bearing test |
|
To check for internal damage of a motor or a gearhead, you can remove power and disassemble the motor from gearhead, then manually rotate the shaft clockwise and counterclockwise. If the motor or gearhead is damaged, you would feel a different resistance from one direction to another, hear abnormal noise, or not be able to rotate the shaft at all. |
How early the life may end will be proportional to how much these specifications are exceeded by and how long. For example, since our ball bearings are rated for 10,000 hour life, exceeding either radial or axial load specifications by 10% may reduce its life by about 1,000 hours.
If you're interested in a service life estimation based on bearing life, please contact our knowledgeable technical support engineers.
| How Are These Specifications Shown? |
Manufacturers may show these specifications differently. Typically, a table (see example below) lists permissible radial loads and axial loads according to the gearhead size and the gear ratio. While the permissible axial load remains the same, the permissible radial load varies by the "distance from the end of the gearhead output shaft".
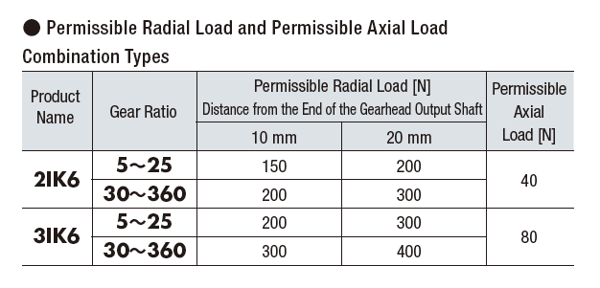
PS: This table lists permissible radial and axial loads only for common geared AC motors. When a chain, gear, belt, etc. is used as the transmission mechanism, the radial load is always applied on the gearhead shaft. For stepper motors, the permissible radial and axial loads for the motors are shown.
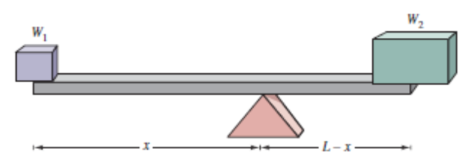
| The "SeeSaw / Fulcrum" Effect (for Radial Load) |
In the above table, you can see that the radial load changes according to the "distance from the end of the gearhead output shaft". This is the distance from the end of the load shaft to the point at which force is applied to the shaft (also the location of the installed load). The permissible radial load increases as the distance from the end of the shaft increases because this also means that the load is closer to the support bearing located right inside the gearhead flange. More load can be supported if the load is "hung" closer to the support bearing, which is the fulcrum is this case.
A "seesaw / fulcrum" is typically used to explain this concept.
Static and Dynamic Radial and Axial Loads
Similar to dynamic and static moment loads, a radial load or an axial load also have both dynamic and static components. The table above is used to determine both.
For example, a static radial load includes the weight of the pulley and belt tension at rest. A dynamic radial load, which requires calculation, includes forces from the same pulley weight and belt tension while in motion. A static axial load would be the weight of the pulley if the motor shaft is in the vertical orientation. A dynamic axial load would be lower than the static axial load, so typically only the static axial load is considered. Make sure that the values are under the published values in the chart.
| TIP: Remember to include belt tension as radial force |
| Remember to size for belt tension! In my good old days as a technical support engineer, excessive belt tension was the cause of motor problems in many occasions. |
To ensure proper handling of all radial and axial loads, make sure these conditions are true:
- The static radial load is under the value in the chart.
- The dynamic radial load is under the value in the chart.
- The static axial load is under the value in the chart.
| The Equation For Dynamic Radial Loads |
For radial loads, there is an addtional component of "dynamic" radial load, which is the radial load when in motion. Also make sure the calculated value is under the value in the chart (see above).
When pulleys, belts, gears, sprockets, chains, etc. are used as the transmission mechanism, the dynamic radial load is calculated with the following equation.
W = T / y
With a belt conveyor, the motor torque provides the driving force that generates work. This is shown as T, which is the amount of torque in N·m. If we consider y (effective radius in meters) to be the radius of the pulley, then we can calculate radial load or W (amount of work).
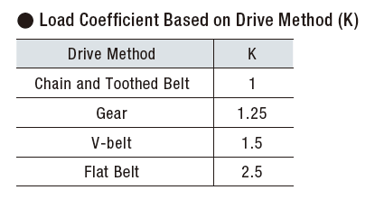
The actual equation is slightly more complicated as load coefficient and service factor are considered.

Other factors, such as drive method and load type, need to be considered for radial load. When using a flat belt drive method, for example, the radial load value increases.
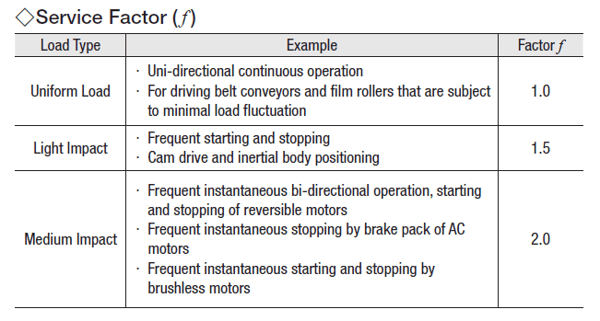
As for service factor, which relates to operating conditions, factors such as frequent starting and stopping of the load as well as changing of rotation direction can affect the radial load.
OK time for some practice.
| Example: Calculating radial load of a conveyor |
Take a look at the belt conveyor application example below. How would you calculate the value of required radial load that you'll need from the motor?
I'm working on a chain and toothed (sprocket) conveyor and using a 2IK6 motor with 360:1 gearhead. I need 10 N·m of torque on an 0.1 meter (effective) diameter sprocket. I'm guesstimating that the chain tension is about 10 N. I only intend to rotate in one direction. My sprocket is mounted 10 mm from the end of the shaft.
Can my gear motor handle the radial and axial load from my application?
The first questions I ask myself is: what equation do I use (we know this), and do I have all the variables?
Since we live in a perfect world, all the variables that are necessary for the calculation are laid out and provided in the preferred units. In reality, it usually takes more work. For example, notice that the load coefficient and the service factor were not given, but the drive method and type of load were given. Also, the values provided may be in different units, so an extra step of unit conversion may be needed.
Once again, we need to:
Make sure these conditions are true:
- The static radial load is under the value in the chart.
- The dynamic radial load is under the value in the chart.
- The static axial load is under the value in the chart.

| Static Radial Load = OK |
Static radial load would be belt tension. The 10 N was a guesstimate, but that's the best information we have right now, so we'll use it. At 10 mm from the end of the shaft, our maximum radial load for the 2IK6 motor is 200 N, so we're good here.
| Dynamic Radial Load = OK |
Plug in values for every variable in the equation for dynamic radial load.
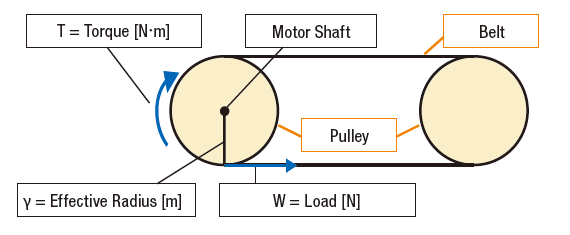
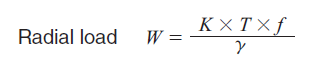
W = what we're solving for in radial load in Newtons.
K = 1; chain and toothed belt conveyor
T = 10 N·m
f = 1; uniform load / unidirectional continuous operation
y = effective radius of pulley = 0.1 meter (effective radius is where the belt contacts the pulley surface)
W = K x T x f / y
W = 1 x 10 x 1 / 0.1
W = 100 N
100 N is below the 200 N permissible radial load value, so we're good here.
| Static Axial Load = OK |
Static axial load is actually unknown at this point, but looking at the application image, we should not have a lot of static axial load, and it definitely should be below the 40 N value in the chart, so we're good here, too.
| Conclusion |
The 2IK6 motor with 360:1 gear ratio gearhead will be able to handle both radial and axial loads.
Most motor sizing software do not consider axial or radial loads, so don't forget to confirm your radial load and axial load after sizing your motor.
| Let Us Help! |
In most cases, a thorough motor sizing takes more work than you think. If your time is as valuable as we think it is, let our experts help!
To begin your motor sizing consultation with us, please use our  , select one of the common applications (shown below), then fill in the blanks. A sizing report, including calculations, can be generated. Our knowledgeable technical support engineers are more than happy to analyze your motor sizing report with you to make sure you buy the right motor the first time (we do not like RMAs either).
, select one of the common applications (shown below), then fill in the blanks. A sizing report, including calculations, can be generated. Our knowledgeable technical support engineers are more than happy to analyze your motor sizing report with you to make sure you buy the right motor the first time (we do not like RMAs either).
As I have mentioned before, a successful motor sizing is only as good as the information provided. Users often oversize motors because either they do not know the exact information necessary for sizing, or they want to extend the life of the motor.
In the next post, I will provide some  . Here's also a post explaining how to
. Here's also a post explaining how to  .
.
|
TIP: Is there an easier way to size motors? |
|
Use a motor sizing tool. After completing a motor sizing, our technical support engineers are able to walk you through the product selection process if necessary. Example: Index Table |







